Order in the Real Numbers
The law of trichotomy states that, for two numbers a and b, one and only one of the following is true.
a = b a equals b
a < b a is less than b
a > b a is greater than b
The law of trichotomy
Category: Mathematics
Mathematics uses many concepts in threes. The first structure mathematically is a triangle. There are acute, right, and obtuse angles. Trigonometry is the study of the relationship of the sides of a triangle. Have your heard of Pascal's Triangle?
Pythagorean triple
A Pythagorean triple consists of three positive integers a, b, and c, such that a2 + b2 = c2. Such a triple is commonly written (a, b, c), and a well-known example is (3, 4, 5). If (a, b, c) is a Pythagorean triple, then so is (ka, kb, kc) for any positive integer k. A primitive Pythagorean triple is one in which a, b and c are coprime (that is, they have no common divisor larger than 1). For example, (3, 4, 5) is a primitive Pythagorean triple whereas (6, 8, 10) is not. A triangle whose sides form a Pythagorean triple is called a Pythagorean triangle, and is necessarily a right triangle.
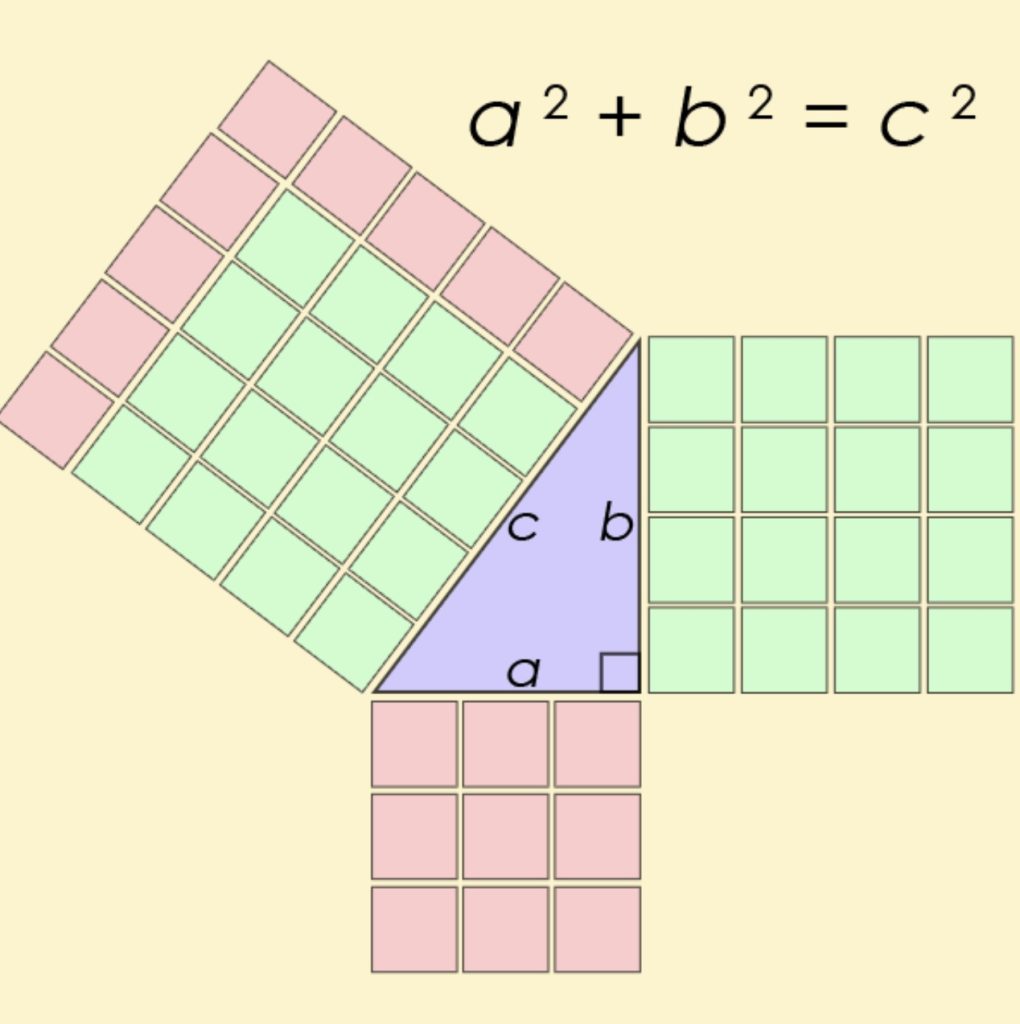
The name is derived from the Pythagorean theorem, stating that every right triangle has side lengths satisfying the formula a2 + b2 = c2; thus, Pythagorean triples describe the three integer side lengths of a right triangle. However, right triangles with non-integer sides do not form Pythagorean triples. For instance, the triangle with sides a=b=1 and c=2 is a right triangle, but (1,1,2) is not a Pythagorean triple because 2 is not an integer. Moreover, 1and 2 do not have an integer common multiple because 2 is irrational.
Pythagorean triples have been known since ancient times. The oldest known record comes from Plimpton 322, a Babylonian clay tablet from about 1800 BC, written in a sexagesimal number system. It was discovered by Edgar James Banks shortly after 1900, and sold to George Arthur Plimpton in 1922, for $10.
One example of a Pythagorean triple is a=3, b=4, and c=5: Ancient Egyptians used this group of Pythagorean triples to measure out right angles. They would tie knots in a piece of rope to create 3, 4, and 5 equal spaces. Three people would then hold each corner of the rope and form a right triangle!
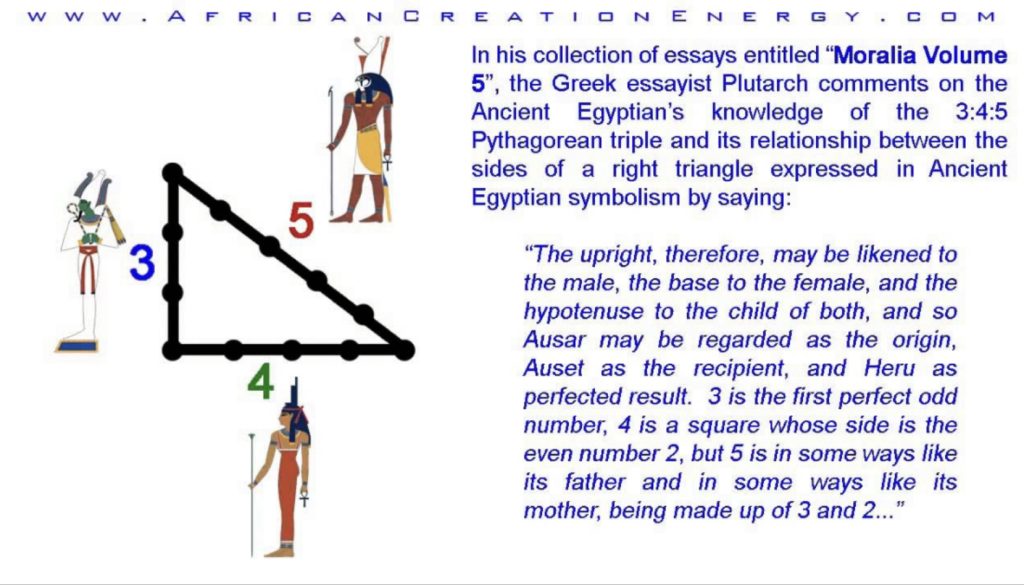
right triangles during the construction process to help determine the slope of the pyramid. The Pythagorean Theorem states that given a right triangle with sides of length a and b respectively and a hypothenuse of length c, the lengths satisfy the equation a2 + b2 = c2.
When searching for integer solutions, the equation a2 + b2 = c2 is a Diophantine equation. Thus Pythagorean triples are among the oldest known solutions of a nonlinear Diophantine equation. The simplest linear Diophantine equation takes the form ax + by = c, where a, b and c are given integers. The solutions are described by the following theorem: This Diophantine equation has a solution (where x and y are integers) if and only if c is a multiple of the greatest common divisor of a and b.
The Three Laws of Recursion
Like the robots of Asimov, all recursive algorithms must obey three important laws:
- A recursive algorithm must have a base case.
- A recursive algorithm must change its state and move toward the base case.
- A recursive algorithm must call itself, recursively.
Recursion is the process of defining a problem (or the solution to a problem) in terms of (a simpler version of) itself. For example, we can define the operation “find your way home” as: If you are at home, stop moving. Take one step toward home.
Let’s begin our discussion of recursion by examining the first appearance of fractals in modern mathematics. In 1883, German mathematician George Cantor developed simple rules to generate an infinite set:
There is a feedback loop at work here. Take a single line and break it into two. Then return to those two lines and apply the same rule, breaking each line into two, and now we’re left with four. Then return to those four lines and apply the rule. Now you’ve got eight. This process is known as recursion: the repeated application of a rule to successive results. Cantor was interested in what happens when you apply these rules an infinite number of times.
Dichotomy paradox – Zeno’s
“That which is in locomotion must arrive at the half-way stage before it arrives at the goal.”
— as recounted by Aristotle, Physics VI:9, 239b10
Suppose Atalanta wishes to walk to the end of a path. Before she can get there, she must get halfway there. Before she can get halfway there, she must get a quarter of the way there. Before traveling a quarter, she must travel one-eighth; before an eighth, one-sixteenth; and so on.
Zeno’s paradox was recursive by cutting the distance in half each time to the infinitesimal. This is also how the Tortoise beat the Hair by questioning time over distance.
Recursive Function Calls
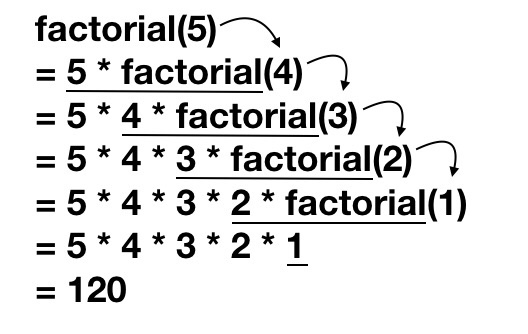
int factorial(int n){ if (n == 1) { return 1; }else { return n * factorial(n-1); } }
A function that does call others is called a nonleaf function. … The factorial function can be rewritten recursively as factorial(n) = n × factorial(n – 1). The factorial of 1 is simply 1. The image shows an object trace of the factorial function written as a recursive function. Each call goes in the run time stack until the base case is reached, and the the stack is popped as the result is passed to each function on the stack.
What Is a Fractal?
The term fractal (from the Latin fractus, meaning “broken”) was coined by the mathematician Benoit Mandelbrot in 1975. In his seminal work “The Fractal Geometry of Nature,” he defines a fractal as “a rough or fragmented geometric shape that can be split into parts, each of which is (at least approximately) a reduced-size copy of the whole.”
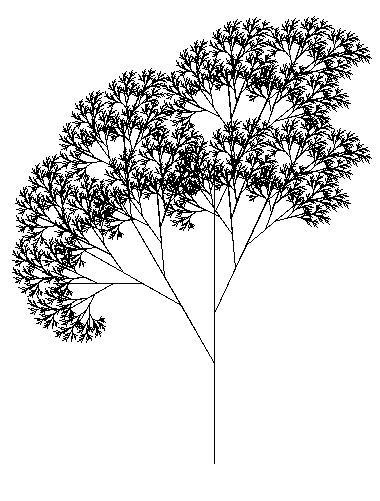
Looking closely at a given section of the tree, we find that the shape of this branch resembles the tree itself. This is known as self-similarity; as Mandelbrot stated, each part is a “reduced-size copy of the whole.”
The Three Laws of Robotics
Isaac Asimov was an American writer and professor of biochemistry at Boston University. During his lifetime, Asimov was considered one of the “Big Three” science fiction writers, along with Robert A. Heinlein and Arthur C. Clarke. A prolific writer, he wrote or edited more than 500 books.
- A robot may not injure a human being or, through inaction, allow a human being to come to harm
- A robot must obey the orders given it by human beings except where such orders would conflict with the First Law
- A robot must protect its own existence as long as such protection does not conflict with the First or Second Laws
Partial sources: https://natureofcode.com/book/chapter-8-fractals/, Wikipedia, Google
