Magic Square

by Allan Adler

A magic square is an arrangement of the numbers from 1 to n^2 (n-squared) in an nxn matrix, with each number occurring exactly once, and such that the sum of the entries of any row, any column, or any main diagonal is the same. It is not hard to show that this sum must be n(n^2+1)/2.

The simplest magic square is the 1×1 magic square whose only entry is the number 1.

The next simplest is the 3×3 magic square and those derived from it by symmetries of the square. This 3×3 square is definitely magic and satisfies the definition given above

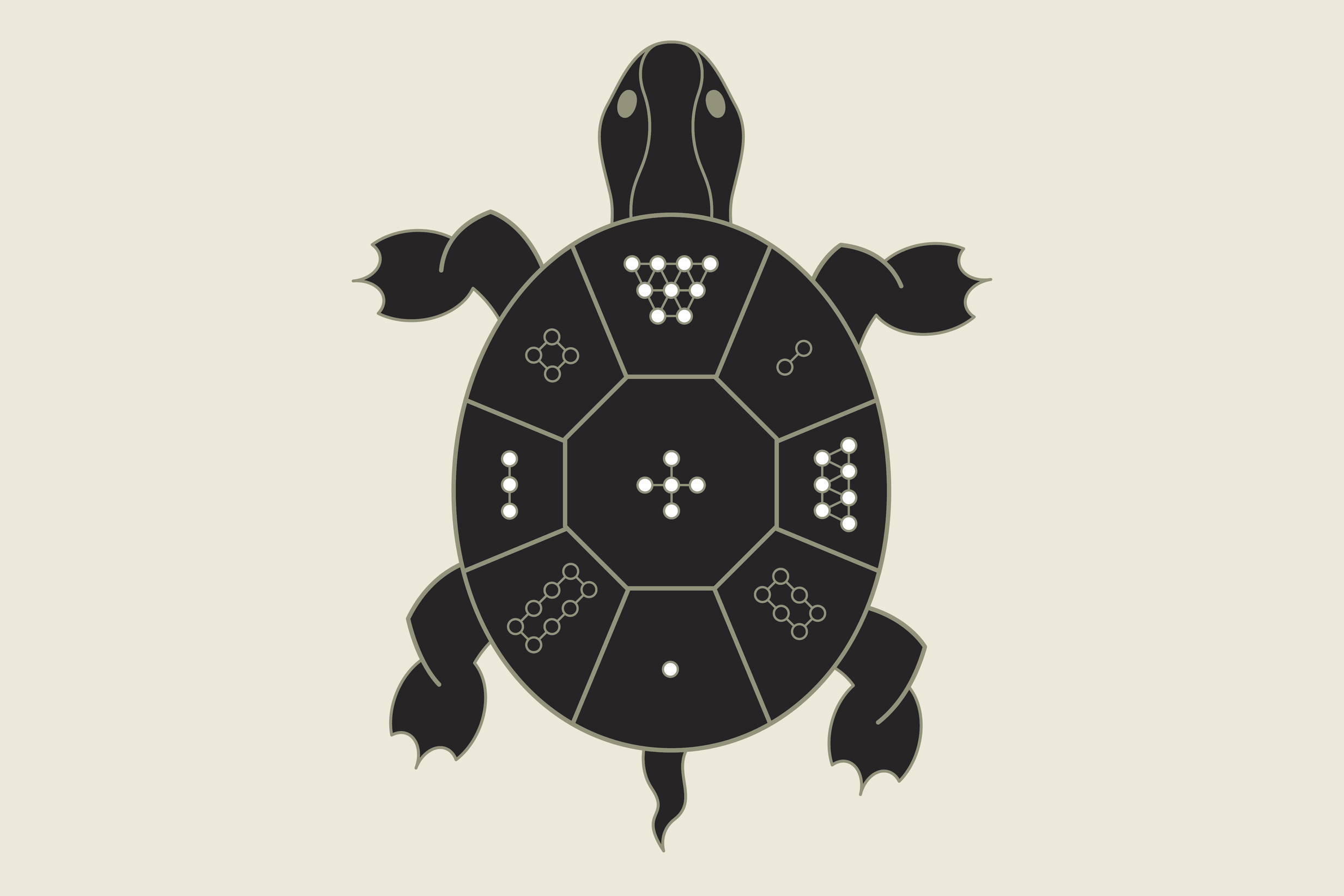
Lo Shu Magic Square Magic squares have been around for over 3,000 years. They are descendants of the oldest known number mystery, the legend of Lo Shu, found in China in a book entitled Yih King.

To learn more about the legend of Lo Shu I wrote to Professor Mutsumi Suzuki formerly of Japan’s Tohoku University, who sent my question on to Philip I. S. Lei, what at the time was a Master of Philosophy student in the Computer Science Department of the Hong Kong University of Science and Technology. Here is Mr. Lei’s response:

The story of ‘Lo Shu’ is as follows:
In the ancient time of China, there was a huge flood. The people tried to offer some sacrifice to the ‘river god’ of one of the flooding rivers, the ‘Lo’ river, to calm his anger. However, every time a turtle came from the river and walked around the sacrifice. The river god didn’t accept the sacrifice until one time, a child noticed the curious figure on the turtle shell. Hence they realized the correct amount of sacrifice to make (15).
The word ‘Shu’ means books.

Can you see why the ‘magic number’ is 15?